Pascals driehoek
In Pascals Driehoek, is ieder getal de som van de twee getallen erboven. De getallen aan het einde van iedere rij zijn altijd 1.
Rij 1: 1 1
Rij 2: 1 2 1
Rij 3: 1 3 3 1
Rij 4: 1 4 6 4 1
Rij 5:
1 5 10 10 5 1
Rij 6:
1 6 15 20 15 6 1
︙
Iedere 15 in Rij 6 is bijvoorbeeld de som van de 5 en 10 erboven.
- Schrijf Rij 7 van Pascals Driehoek op.
- Schrijf een
volgende rijblok dat een rij van Pascals Driehoek als invoer heeft en de volgende rij rapporteert:
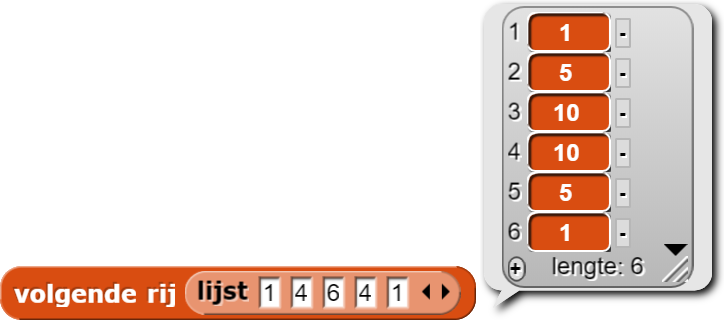
Om naar een specifiek getal in Pascals Driehoek te verwijzen heb je de rij en kolom van dat getal nodig.
Rijen zijn simpel; kolommen zijn lastiger door de vorm van de driehoek. Dit is Pascals Driehoek, verdeeld
in kolommen:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
- Welk getal staat er in rij 6, kolom 2?
- Twee getallen in rij 5 worden opgeteld om het getal in rij 6, kolom 2 te krijgen. Wat zijn de locaties van deze getallen?
- Om te bepalen wat het getal in rij 14, kolom 8 is van Pascals Driehoek, moet je twee getallen van rij 13 weten. In welke kolommen staan deze getallen van rij 13?
Pascals Driehoek telt het aantal manieren om een verzameling van een grotere verzameling te pakken. Stel je hebt 3 vruchten: een appel, een banaan en een citroen, we korten deze even af naar A, B en C. We kunnen nu een kleinere groep uit deze verzameling pakken. De kleine verzameling heeft 0 vruchten, het klinkt misschien gek, maar er is maar één manier om geen vruchten te pakken. Stel je wil 1 vrucht pakken uit deze verzameling, dan zijn er 3 mogelijkheden, alleen A, alleen B of alleen C. Stel dat je er 2 wil pakken, dan zijn er ook 3 mogelijkheden: AB, AC of BC. Als je er 3 wil pakken is er maar één mogelijkheid, alledrie. Deze 4 mogelijkheden kan je aflezen in Pascals Driehoek op de 4e rij: 1,3,3,1. De rij geeft aan hoe groot je verzameling, de eerste rij voor een verzameling van 0 elementen, de tweede rij voor 1, de derde voor 3 etc. De positie in de rij zegt hoeveel je wil pakken. Je moet niet vergeten dat de rij en positie bij 0 begint. Stel dus dat je 6 vruchten hebt en je wil weten hoeveel mogelijkheden er zijn om er 4 te pakken, kijken we in de 7e rij op de 5e positie. Op die positie staat het getal 15. Je kan dit altijd zelf narekenen, al wordt dit voor grote getallen wel heel lastig.
- Schrijf een
pascalblok dat twee getallen als invoer heeft, rij en kolom, en daarmee de waarde in Pascals Driehoek op die locatie rapporteert.