Hoofdstuk 5 Les 3: Tijdexperimenten, Pagina 2

Timing-rapporteurs

Op deze pagina, ga je een algoritme-timer maken om de efficiëntie van algoritmes te vergelijken.

De titel van deze pagina heeft twee betekenissen: Je bouwt een "timing-rapporteur" die rapporteurs timet.

Snap! stelt ons in staat om te melden hoe lang het duurt voordat een programma is voltooid.

Zoek in het Waarnemenpalet voor de huidig(e) (datum)-rapporteur. Sleep het in het scriptgebied. Selecteer van het invoermenu tijd in millisecondes.

Klik meerdere keren op het blok. Let op de resultaten.
Open het "H5L3-RapporteurTimer"-project dat je hebt opgeslagen op de vorige pagina.
Download deze library: U5L3functiontimer.xml, en sleep het bestand in je Snap!-applicatie om het te importeren.

Aan de onderkant van het Variabelenpalet staat een blok dat time function heet. Het heeft als invoer een rapporteurblok (met invoeren al ingevuld). Wanneer je het blok aanklikt dan voert het zijn invoerblok uit, berekent het resultaat en rapporteert hoe lang het duurde om de berekeningen te doen (in milliseconden).

Je kan het lijst vanblok vervangen met iedere rapporteur. Je kan time function aanpassen om te leren hoe het werkt.

In dit voorbeeld duurde het 16660 milliseconden om de lijst met gehele getallen van 1 tot 1000 te berekenen. (Het aantal dat je ziet, hangt af van hoe snel je computer is en welke andere programma's erop worden uitgevoerd.)

Dit is hoe time function werkt:
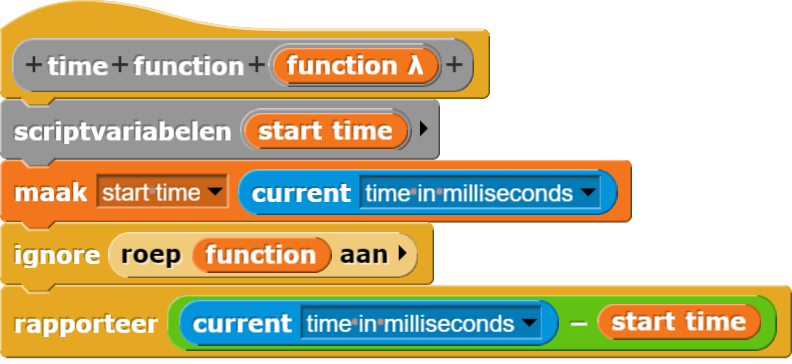
Geen Afbeelding

Het maakt een variabele dat start time heet en en zet het gelijk aan de huidige tijd.
Het roept de rapporteur aan waar van je de tijdsduur wilt weten en negeert het resultaat van de rapporteur.
Wanneer de rapporteur klaar is pakt het weer de huidige tijd en trekt het af van de start time.

Gebruik time function om Alex' en Bo's manieren van getallen van 1 tot n optellen te vergelijken. Probeer het met een aantal verschillende grote getallen om te zien hoe verschillend de algoritmes zijn qua tijd om de uitkomst te berekenen.

Alex' en Bo's algoritmes lossen hetzelfde probleem om maar zijn vrij verschillend qua efficiëntie. Stel je het verschil voor wanneer je getallen van 1 tot 1.000.000 optelt...

De efficiëntie van een algoritme maakt een groot verschil. Soms kan je niet anders dan een efficiënt algoritme gebruiken om grote varianten van een probleem op te lossen.

In Les 1 , heb je twee rapporteurs gebouwd die de positie van een element in een lijst geven:

Een lineaire zoekopdracht betekent dat je de lijst doorzoekt waarbij je langs ieder element loopt.

Een binaire zoekopdracht betekent dat je een gesorteerde lijst in twee helften verdeelt bij iedere stap.
- De rapporteur positie van getal in ongesorteerde lijst werkt voor elke lijst door element-voor-element de lijst te doorzoeken tot je een match vindt. Dit heet een lineaire zoekopdracht omdat het programma van het begin van de lijst in een rechte lijn zoekt tot hij een match vindt.
- De rapporteur positie van getal in gesorteerde lijst werkt op gesorteerde lijsten door herhaaldelijk de lijst te verdelen in twee delen van gelijke grootte en gebruikt de middelste waar om te beslissen welke helft nu doorzochtgaat worden om de match te vinden. Dit heet een binaire zoekopdracht omdat binair "twee" betekent en het algoritme de lijst in twee delen verdeelt.
Beide werken op gesorteerde lijsten. Vergelijk ze voor een aantal lange gesorteerde lijsten en maak een tabel van je bevindingen. Mogelijk moet je zeer grote lijsten gebruiken, bijvoorbeeld met 1000 of 2000 elementen, om betekenisvolle resultaten te krijgen. Welk algoritme is sneller?
Is het andere algoritme ooit sneller?
In de hele cursus heb je veel algoritmes gemaakt. Vergelijk hun tijdsduur, hier zijn een paar voorbeelden:
- (zoals je zag bij Hoofdstuk 3 Les 4: Een diagram-app maken)
- (zoals je zag bij Hoofdstuk 5 Les 1: Algoritmes om lijsten te verwerken)
- (zoals je zag bij Hoofdstuk 5 Les 3: Algoritmes vergelijken)
Controleer de tijdsduur van deze algoritmes met invoer van verschillende grootte en beschrijf het gedrag dat je ziet. Hoe groter je de invoer maakt hoe meer je te weten komt over de efficiëntie.
"H5L3-Timer"