Hoofdstuk 5 Les 4: Onoplosbare en onbeslisbare problemen, Pagina 2

Een onbeslisbaar probleem

Op deze pagina, ga je een probleem bekijken dat geen antwoord kan hebben.

Op dit punt in de cursus heb je de frustratie ervaren van het debuggen van een programma. Het zou geweldig zijn als er een algemeen foutopsporingsprogramma was dat code kon lezen en daarna bepalen of er bugs in zitten. Helaas kunnen we een bewijs uit het ongerijmde gebruiken (zoals Alex, Bo en Yasmine op de vorige pagina deden) om te bewijzen dat dit niet kan.

Eerst gaan we ervan uit dat het mogelijk is om een functie te schrijven die bepaalt of er oneindige lussen in een programma zitten (situaties waarin een functie voor altijd wordt uitgevoerd zonder een waarde te rapporteren). Vervolgens zullen we die functie gebruiken in een programma dat speciaal is ontworpen om een tegenstrijdigheid te creëren om te bewijzen dat de aanname onjuist is: er kan geen programma voor algemene foutopsporing bestaan . "Heeft dit programma fouten" is een onbeslisbaar probleem ; er kan nooit een algoritme worden gebouwd dat deze vraag voor elk programma beantwoordt.

Een oneindige lus is een rij computerinstructies die zichzelf voor altijd blijft herhalen.

Een onoplosbaar probleem is een probleem waarvoor geen enkel algoritme geschreven kan worden om de oplossing te vinden.

Een onbeslisbaar probleem is er een waarvoor geen algoritme kan worden geschreven dat altijd een juiste waar/onwaar-beslissing geeft voor elke invoerwaarde. Onbeslisbare problemen zijn een subcategorie van onoplosbare problemen dat alleen problemen bevat die een ja/nee-antwoord zouden moeten hebben (zoals: bevat mijn code een bug?).

Aannemen dat een `stopt?`-functie bestaat

De aanname maken

We kunnen de code in stopt? niet weergeven; we bewijzen dat het helemaal niet kan worden geschreven, ongeacht hoe het geïmplementeerd wordt.

Ten eerste nemen we aan dat er een functie bestaat met de naam stopt? die bepaalt of een bepaalde rapporteur een waarde in een eindige hoeveelheid tijd rapporteert. (Als dat zo is, zeggen we dat de rapporteur stopt. ) Er zijn twee invoeren nodig: een functie en een invoerwaarde voor die functie. Het rapporteert waar als de functie een waarde zou rapporteren wanneer die invoer wordt gegeven; het rapporteert niet waar als de functie voor altijd zou worden uitgevoerd (in een oneindige lus).
Geen Afbeelding

De functie afgerond bijvoorbeeld wordt niet voor altijd uitgevoerd met de invoer 7.5; het zal 8 rapporteren.

De grijze ring om de invoerfunctie heen betekent dat de stopt? de invoerfunctie als data ziet in plaats van het uit te voeren.

Geen Afbeelding omdat een waarde rapporteert.

Stel je anderzijds voor dat we een programma hebben dat in een oneindige lus komt te zitten met de invoer foo; dit programma zal nooit stoppen en dus nooit iets rapporteren.

Geen Afbeelding omdat zich oneindig herhaalt.

Het plan voor het bewijs bekijken

We zullen bewijs uit het ongerijmde gebruiken om te laten zien dat de volgende vraag niet beantwoord kan worden in het algemeen:

Zal een bepaald computerprogramma, met een bepaalde invoer, een resultaat rapporteren in een eindige hoeveelheid tijd?

Het "computerprogramma" is de eerste invoer voor stopt?. De 'gegeven invoer' is de tweede invoer. stopt? rapporteert oftwel waar oftewel onwaar: het computerprogramma zal stoppen of het zal niet stoppen.

Merk op dat stopt? zelf altijd een resultaat moet rapporteren, zelfs als het programma dat het test dat niet doet. Dit is zo omdat we aannemen (waarvan we gaan laten zien dat het niet klopt) dat stopt? altijd werkt, dat het altijd een antwoord rapporteert.

We kunnen deze vraag beantwoorden voor specifieke functies, maar we willen bepalen of we een algemene test kunnen maken die ons vertelt of een bepaalde functie een waarde rapporteert voor een specifieke invoer.

Wat betekent het dat we de vraag kunnen beantwoorden voor specifieke functies?

Het deel "in het algemeen" is belangrijk. Natuurlijk kunnen we de vraag beantwoorden voor bepaalde programma's. Deze stopt voor elke invoer:

Deze stopt voor geen enkele invoer:

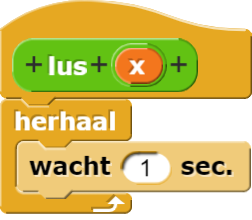
Deze stopt soms, voor elke invoer behalve 87:

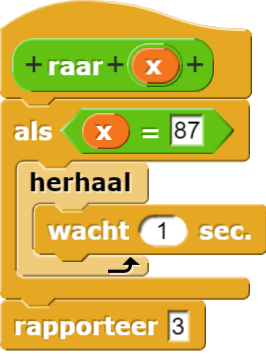
Herinner je dat de vraag is of we een test kunnen maken die ons zegt of elke functie een waarde rapporteert voor elke invoer.

1. Beschrijf het proces van een bewijs uit het ongerijmde.
2. Beschrijf wat de stopt?functie doet.
3. Beschrijf hoe je de stopt?functie in dit bewijs gaat gebruiken.

Laten zien hoe dit een tegenstrijdigheid creëert

Een programma maken waarvoor `stopt?` niet werkt

Om te bewijzen dat een dergelijke functie niet kan bestaan, moeten we een tegenstrijdigheid creëren. We moeten aantonen dat er ten minste één functie en één invoer voor die functie moet zijn waarvoor stopt? niet werkt zoals we dachten dat het werkt. Dus we kunnen een blok, tester maken, specifiek om stopt? te breken:

Net zoals dat de # en ⋮ symbolen zijn voor invoeren als getallen of lijsten, is λ niet deel van de naam van de invoer maar een type-hint die gemaakt wordt wanneer het rapporteur invoertype wordt geselecteerd:
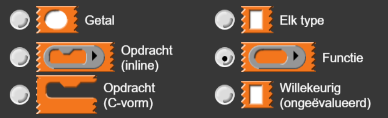
Geen Afbeelding

Herinner je dat dat een invoertype selecteren het uiterlijk van het invoervak aanpast zodat het het aangeeft welke invoer er verwacht wordt. Het invoervak voor tester zal een afgeronde grijze ring hebben om aan te geven dat de invoer een rapporteur moet zijn: Geen Afbeelding

Het herhaalblok in dit script zorgt voor een oneindige lus. Als de testercode in dit deel van het alsblok komt, dan zal het nooit iets rapporteren. Dus of tester zichzelf zal stoppen hangt af van de uitkomst van het stopt?predikaat in het alsblok.

Het blok Geen Afbeelding vraagt wat er gebeurt als we de ingevoerde functie (rapporteur) aanroepen met zichzelf als invoer. Dit is vergelijkbaar met toen Bo een zin maakte over de zin die ze aan het maken was met de zin "De zin die ik nu zeg is onjuist."

Dit is uitdagend. Blijf volhouden! We zijn een tegenstrijdigheid aan het maken om te bewijzen dat de stopt?functie die aangeroepen wordt in tester niet kan bestaan.

Zelf-verwijzing gebruiken om een tegenstrijdigheid te maken

Om precies de situatie te creëren die Bo uitlegde ("De zin die ik nu zeg is onjuist."), gaan we tester aanroepen over zichzelf:
Geen Afbeelding
Het als blok in het testerblok zal nu vragen of tester zal stoppen (niet voor altijd doorgaan) als het aangeroepen wordt met tester als invoer. Het predikaat in het alsblok zal stopt? (tester) (tester) zijn.

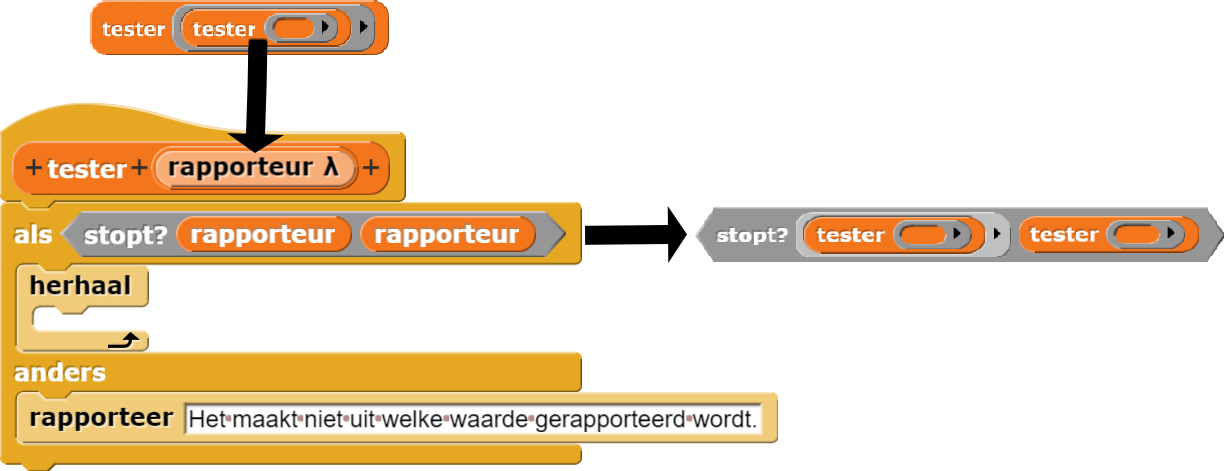
Dus net als in de voorbeelden hierboven,

Geen Afbeelding zou betekenen dat een waarde geeft.

Geen Afbeelding zou betekenen dat voor eeuwig blijft herhalen.

De Tegenstrijdigheid Begrijpen

Wanneer we Geen Afbeelding aanroepen, zien we een tegenstrijdigheid. Om te zien hoe, kijken we naar de definitie van tester:

Om te laten zien dat het resultaat fout moet zijn voeren we een gevalanalyse uit net zoals we deden op pagina 1. Kijk naar de twee mogelijke gevallen:

Als dan zal tester de eerste aanpak van de als nemen en dus voor altijd herhalen. Dat betekent dat niet zal stoppen en dus geeft stopt? het foute antwoord.
Als dan zal tester de elseaanpak nemen en "Het maakt niet uit welke waarde gerapporteerd wordt." rapporteren. Wat betekent dat wel zal stoppen en dus heeft stopt? het weer fout.

Het maakt niet uit welke waarde tester rapporteert, alleen maar dat het een waarde rapporteert, maar het maakt wel uit welke waarde stopt? rapporteert.

Bij alles wat stopt? rapporteert zal het nooit overeenkomen met zichzelf bij een programma zoals dit. Deze tegenstrijdigheid (deze logische onmogelijkheid) betekent dat de aanname dat het mogelijk is stopt? te maken, fout is. . Dit is niet alleen een claim over wat er zou gebeuren in Snap !. De taal die je gebruikt om een computerprobleem te onderzoeken, kan de duidelijkheid of leesbaarheid van je code beïnvloeden, maar niet of er een oplossing voor een probleem bestaat. Zelfs met de vooruitgang in kwantumcomputers, zullen we nooit in staat zijn om een programma voor algemene foutopsporing te maken. Dit beroemde voorbeeld staat bekend als het stopprobleem, en het feit dat het stopprobleem onbeslisbaar is, is de Halting Theorem (Stopstelling).

Neem dit hele bewijs opnieuw samen door. Zorg ervoor dat jij en je partner het volgende begrijpen:
1. Alles uit opdracht 1 over bewijs door tegenstrijdigheid, wat stopt? doet en hoe stopt? wordt gebruikt in het bewijs.
2. De basisprincipes van hoe de functie tester zich gedraagt (voor elke functie die wordt ingevoerd).
3. Hoe het aanroepen van leidt tot een tegenstrijdigheid.
4. Wat die tegenstrijdigheid betekent in het bewijs.
5. Of het stopprobleem een onoplosbaar probleem is, een onbeslisbaar probleem, of beide; en why.
Schrijf een paragraaf waarin het verschil wordt uitgelegd tussen een probleem dat niet kan worden opgelost (zoals het stopprobleem) en een probleem dat ongelooflijk veel tijd kost.

Wie bewees voor het eerst de Halting Theorem (Stopstellling)?

Alan Turing (1912-1954) was een van de grondleggers van de informatica. Hij staat bekend om twee prestaties. Ten eerste heeft hij een enorme bijdrage geleverd aan het winnen van de Tweede Wereldoorlog door een wiskundige theorie en bijbehorende machine uit te vinden om de gecodeerde berichten van de Duitse Enigma-machine te breken. Ten tweede was Turing samen met zijn collega Alonzo Church een oprichter van theoretische informatica : bewijzen hoe computers moeten werken ongeacht de toekomstige technologie. Door zijn werk aan het stopprobleem, bewees hij dat er berekeningen zijn die nooit gedaan kunnen worden , ongeacht hoe groot en snel de computer is.

Toen Turing dit werk deed, waren er geen programmeerbare computers; mensen moesten fysieke machines opnieuw bedraden om elk nieuw probleem op te lossen. Met krachtige programmeertalen (zoals Snap ! ) kunnen we de essentie van het bewijs van Turing veel gemakkelijker zien en begrijpen omdat we functies kunnen gebruiken als invoer voor andere functies, zoals je hebt gezien met map , houd en combine . Dit bewijs was nog moeilijker voor Turing omdat hij het idee moest uitvinden van een computerprogramma dat kan worden weergegeven als gegevens in de computer.